Introducción.
|
El
control PID, siglas que denotan control Proporcional
- Integral - Derivativo, viene
despertando el interés del diseñador desde los
primeros desarrollos del control automático, aunque se
carecía entonces de la infraestructura digital actual.
Desde un punto de vista teórico, la
implementación de este tipo de control siempre
resultó atractiva y en la actualidad disponemos ya de la
tecnología digital avanzada que ha permitido la
construcción de los microcontroladores PIDs.
|
 |
 |
Norma de control P.I.D.
|
A
continuación se expone la norma de control PID.
|
| En
un controlador PID, la acción del control se genera como una
suma de tres términos, que matemáticamente se
expresa: |
|
(1)
u(t) = uP(t) + uI(t)
+ uD(t)
|
Donde
uP
representa la parte
proporcional, uI es la parte
integral y uD la parte
derivativa.
|
| Control
proporcional. |
| La
parte proporcional indica una realimentación de ganancia. |
|
(2)
uP(t) = Ke(t)
|
| Siendo
e el
error de control, y K
la ganancia del controlador. El error se define como la diferencia
entre el punto del valor establecido como ideal ysp y la salida
efectiva del proceso y, en forma: |
|
(3)
e(t) = yp(t) + y(t)
|
| Sustituyendo
(3) en (2) nos queda: |
|
(4)
uP(t) = K(bysp(t)) -
y(t)
|
Donde
al coeficiente b lo
llamamos "ponderación del valor ideal", que es el que
permite el ajuste independiente de la respuesta del "punto del valor
ideal" y la respuesta de variación de carga.
Control integral. |
| El
controlador proporcional generalmente añade al sistema un
"error de estabilización". La acción integral se
introduce para eliminar este error y toma la forma: |
|
(5)
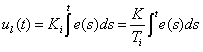
|
 |
 |
Reinicio automático.
|
| Como
indicamos anteriormente, un control proporcional añade un
"error de estabilización". Para eliminarlo se puede
añadir un término de reinicio ajustable, aplicado
manualmente a la señal de control. El control proporcional
dado por la ecuación (2) se convierte entonces en: |
|
(6)
up(t) = Ke(t) - ub(t)
|
Donde
ub es el
término de reinicio.
Históricamente, la acción integral fue el
resultado de un intento por obtener el ajuste automático del
término de reinicio.
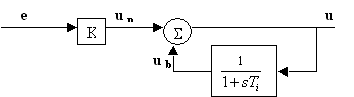
En forma gráfica se puede entender consultando la siguiente
figura:
|
|
|
|
Figura
1.1
|
| La
idea es filtrar la parte baja de la frecuencia de la señal
de error y añadir ésta a la parte proporcional.
Nótese que el lazo cerrado tiene realimentación
positiva. Analíticamente, el sistema de la figura se puede
expresar: |
|
(7)
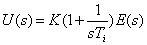
|
| Lo
que representa la respuesta de un controlador proporcional-integral
(PI). De esta manera, tenemos: |
|
(8)
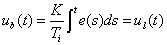
|
Él
reinicio automático es entonces lo mismo que
la acción integral. Nótese, sin embargo, que la
"ponderación del valor ideal" no se genera al obtener la
acción integral como reinicio automático.
Control derivativo
El control derivativo se utiliza para disponer de una acción
anticipativa, es decir, la derivada nos informa de una tendencia que
afectará al futuro, y que se puede analizar y corregir si
procede.
Su forma más sencilla es: |
|
(9)
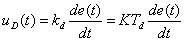
|
| Combinando
ambas acciones, integral y derivativa, resulta: |
|
(10)
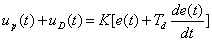
|
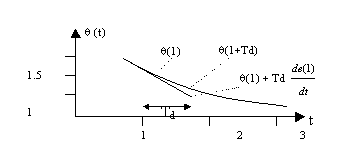
| Esto
significa que la acción de control se basa en la
extrapolación lineal del error Td unidades hacia delante. El
parámetro Td, que denominamos tiempo derivativo, se puede
interpretar en forma intuitiva, observando la gráfica de la
figura 1.2. |
|
|
|
Figura
1.2
|
|
Interpretación
de la acción derivativa como predicción del error
|
La
diferencia principal entre un controlador PID y otros más
complejos radica en que el modelo dinámico permite mejores
predicciones que una extrapolación estrictamente lineal.
Veamos algunos casos:
Para algunas aplicaciones prácticas, el "punto del valor
ideal" es, en general, constante, por ejemplo, el mantenimiento de una
determinada velocidad angular. En este caso, la derivada del "punto del
valor ideal" es cero, excepto para aquellos instantes de tiempo donde
el "punto del valor ideal" es alterado. En estos instantes de tiempo la
derivada puede llegar a ser muy grande y la extrapolación
lineal no resulta útil cuando se utiliza para la
predicción en tales señales.
Tampoco es adecuada, evidentemente, cuando la señal medida
cambia rápidamente en comparación con la
predicción.
Una mejora en la representación de la acción
derivativa es, entonces: |
|
(11)
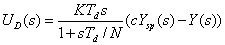
|
| La
señal se pasa a través de un filtro paso-bajo
cuya constante de tiempo es Td / N. El parámetro c es una
"ponderación del valor ideal", que es generalmente puesto a
cero. |
 |
 |
Ponderación del valor
ideal
|
| El
controlador PID introduce ceros extras durante la
transmisión desde el "punto del valor ideal" a la salida. |
| Las
ecuaciones y los ceros del controlador PID pueden ser determinados como
las raíces de la ecuación. |
|
(12)
cTiTds2 + bTis + 1 = 0
|
| Donde
no se dan ceros extras sí b = 0 y c = 0. Si solo c =
0, entonces hay un cero extra para: |
|
(13)
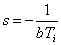
|
| Este
cero puede tener una influencia significativa en la respuesta del
"punto del valor ideal". La sobre oscilación es generalmente
grande para b = 1, y puede ser reducida sustancialmente utilizando un
valor pequeño de b. Esta resulta una solución
mucho mejor que la forma tradicional de sincronizar al controlador. |
| En
la figura 1.3, se muestra un control PI con función de
transferencia. |
|
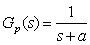
|
|
|
|
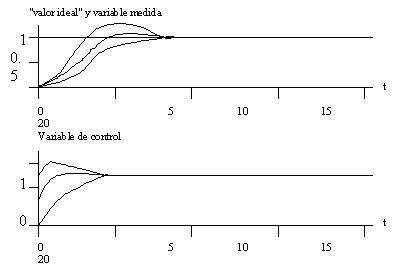
Figura
1.3
|
|
La
utilidad de la "ponderación del valor ideal"
|
|
Los
valores del parámetro de la "ponderación del
valor ideal" son 0, 0.5 y 1
|
 |
|
|
 |
Diferentes representaciones del
controlador P.I.D.
|
| El
controlador PID discutido en la sección anterior puede
ser descrito como: |
|
(14)
U(s) = Gsp(s)Ysp(s) -
Gc(s)Y(s)
|
| Donde: |
|
(15)
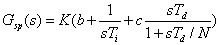
|
|
(16)
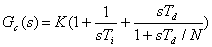
|
| El
comportamiento lineal del controlador se caracteriza entonces por dos
funciones de transferencia: Gsp(s), que representa
la transmisión de la señal desde el "punto del
valor ideal" a la variable de control, y Gc(s), que
describe la transmisión de la señal desde la
salida del proceso a la variable de control. |
| Nótese
que la transmisión de señal
desde la salida del proceso hasta la señal de control es
diferente del camino de la transmisión de señal
desde el "punto del valor ideal" a la señal de control si
para el parámetro "ponderación del valor ideal"
tenemos que b ( 1 o c ( 1. El controlador PID dispone entonces de dos
grados de libertad. |
El
controlador PID se comporta como un algoritmo de control simple que
tiene siete parámetros:
Ganancia del controlador K,
tiempo integral Ti, tiempo
derivativo Td, ganancia
derivativa máxima N,
"ponderación del valor ideal" b
y c y constante de tiempo del
filtro Tf. |
| Los
parámetros K, Ti
y Td, son los
parámetros primarios que normalmente son discutidos. |
| El
parámetro N es una
constante cuyo valor oscila entre 5 y 20. |
| El
parámetro de la "ponderación del valor ideal" b
tiene normalmente los valores 0 o 1, aunque puede tomar otros valores. |
| El
parámetro c
generalmente tiene valor cero para controladores comerciales. |
 |
 |
La forma estándar
|
El
controlador dado por las ecuaciones anteriores está
extraído de la denominada forma estándar o la
forma ISATM (Instrument Society America, por sus
siglas en inglés).
La forma estándar admite ceros complejos, lo cual es
útil al trabajar con sistemas de control con polos
oscilatorios. |
| La
parametrización dada para la ecuación (14) es la
forma habitual, aunque existen otros tipos. |
 |
 |
La forma paralela
|
| Es
una ligera variación de la forma estándar, y se
describe: |
|
(17)
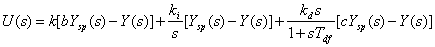
|
Esta
forma tiene la ventaja de que es fácil obtener un
control puramente proporcional, integral o derivativo simplemente
escogiendo los parámetros adecuados con valor a cero.
La interpretación de Ti y Td como tiempo de
integración y tiempo de predicción se pierden en
esta representación. |
| Los
parámetros de los controladores dados por las ecuaciones
anteriores están relacionados por: |
|
(18), (19) y (20)
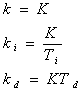
|
La
forma dada por la ecuación (17) se usa
generalmente en cálculos analíticos, debido a la
linealidad de los parámetros. Sin embargo, los
parámetros no tienen una interpretación
física sencilla.
|
 |
 |
La forma serie
|
| Si
Ti > 4Td la función de transferencia Gc(s) puede ser
escrita como. |
|
(21)
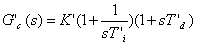
|
| Esta
forma es llamada forma en serie. |
| Si
N = 0, los parámetros se relacionan con la forma paralela en
el siguiente modo: |
|
(22)
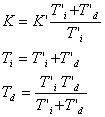
|
| La
relación inversa es: |
|
(23)
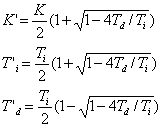
|
| Para
N diferente de 0 se obtienen formulas similares, pero
más complejas. |
| Nótese
que la forma paralela admite ceros complejos,
mientras que la forma en serie tiene ceros reales. |
| La
forma en serie es también llamada la forma
clásica debido a que ésta es la obtenida
naturalmente cuando se implementa un controlador con reinicio
automático. |
 |
 |
Algoritmos de velocidad
|
| Los
controladores PID dados por las ecuaciones vistas son llamados
algoritmos posicionales, debido a que la salida del algoritmo es la
variable de control. |
En
algunos casos es más natural que el algoritmo de control
genere la velocidad de cambio de la señal de control.
Tal ley de control es denominada algoritmo de velocidad.
En diseños digitales, los algoritmos de velocidad se llaman
también algoritmos increméntales.
Algunos controladores primitivos diseñados para el control
de motores utilizaban algoritmos de velocidad.
Estos algoritmos y estructuras se mantuvieron por los fabricantes en
espera de que la tecnología alcanzara el grado de desarrollo
necesario para contar con productos compatibles con la antigua
tecnología.
Sin embargo, existen razones de protección contra efectos
indeseables inherentes al control por los que es importante el
conocimiento y uso de algoritmos de velocidad.
En cualquier caso, no hemos querido dejar de mencionar este punto, aun
sin tratarlo en detalle. |
 |
|

|
|
|


 Semblanza
Breve
Semblanza
Breve 

![]()